Consumer's Equilibrium Through
Indifference Curve Analysis:
Definition:
"The term
consumer’s equilibrium refers to the amount of goods and services which the
consumer may buy in the market given his income and given prices of goods in the
market".
The aim of the consumer is to get maximum satisfaction from his money
income. Given the price line or budget line and the
indifference map:
"A consumer is said to be in equilibrium
at a point where the price line is touching the
highest attainable indifference curve from below".
Conditions:
Thus the
consumer’s equilibrium under the indifference curve theory must meet the
following two conditions:
First:
A given price line should be tangent to an indifference curve or marginal rate
of satisfaction of good X for good Y (MRSxy) must be equal to the
price ratio of the two goods. i.e.
MRSxy = Px / Py
Second:
The second order condition is that indifference curve must be convex to the
origin at the point of tangency.
Assumptions:
The following
assumptions are made to determine the consumer’s equilibrium position.
(i)
Rationality: The consumer is rational. He wants to obtain maximum
satisfaction given his income and prices.
(ii)
Utility is ordinal: It is assumed that the consumer can rank his
preference according to the satisfaction of each combination of goods.
(iii)
Consistency of choice: It is also assumed that the consumer is
consistent in the choice of goods.
(iv)
Perfect competition: There is perfect competition in the market from
where the consumer is purchasing the goods.
(v) Total
utility: The total utility of the consumer depends on the quantities of
the good consumed.
Explanation:
The
consumer’s consumption decision is explained by combining the budget line and
the indifference map. The consumer’s equilibrium position is only at a point
where the price line is tangent to the highest attainable indifference curve
from below.
(1) Budget Line
Should be Tangent to the Indifference Curve:
The
consumer’s equilibrium in explained by combining the budget line and the
indifference map.
Diagram/Figure:
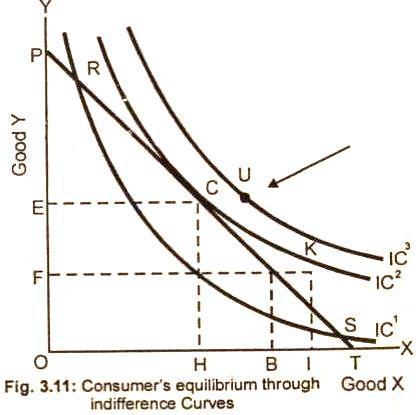
In the diagram 3.11, there are three indifference curves IC1,
IC2 and IC3. The price line PT is tangent to the
indifference curve IC2 at point C. The consumer gets the maximum
satisfaction or is in equilibrium at point C by purchasing OE units of good Y
and OH units of good X with the given money income.
The consumer cannot be in
equilibrium at any other point on indifference curves. For instance, point R and
S lie on lower indifference curve IC1 but yield less satisfaction. As
regards point U on indifference curve IC3, the consumer no doubt gets
higher satisfaction but that is outside the budget line and hence not achievable
to the consumer. The consumer’s equilibrium position is only at point C where
the price line is tangent to the highest attainable indifference curve IC2
from below.
(2) Slope
of the Price Line to be Equal to the Slope of Indifference Curve:
The second
condition for the consumer to be in equilibrium and get the maximum possible
satisfaction is only at a point where the price line is a tangent to the highest
possible indifference curve from below. In fig. 3.11, the price line PT is
touching the highest possible indifferent curve IC2 at point C. The
point C shows the combination of the two commodities which the consumer is
maximized when he buys OH units of good X and OE units of good Y.
Geometrically, at tangency point C, the consumer’s substitution ratio is equal
to price ratio Px / Py. It implies that at point C,
what the consumer is willing to pay i.e., his personal exchange rate between X
and Y (MRSxy) is equal to what he actually pays i.e., the
market exchange rate. So the equilibrium condition being Px / Py
being satisfied at the point C is:
Price of X
/ Price of Y = MRS of X for Y
The
equilibrium conditions given above states that the rate at which the individual
is willing to substitute commodity X for commodity Y must equal the ratio at
which he can substitute X for Y in the market at a given price.
(3)
Indifference Curve Should be Convex to the Origin:
The third
condition for the stable consumer equilibrium is that the indifference curve
must be convex to the origin at the point of equilibrium. In other words, we can
say that the MRS of X for Y must be diminishing at the point of equilibrium. It
may be noticed that in fig. 3.11, the indifference curve IC2 is
convex to the origin at point C. So at point C, all three conditions for the
stable-consumer’s equilibrium are satisfied.
Summing
up, the consumer is in equilibrium at point C where the budget line PT is
tangent to the indifference IC2. The market basket OH of good X and
OE of good Y yields the greatest satisfaction because it is on the highest
attainable indifference curve. At point C:
MRSxy
= Px / Py
Relevant Articles:
|