Marginal Rate of Technical Substitution (MRTS):
Definition:
Prof. R.G.D. Alien and J.R. Hicks
introduced the concept of MRS (marginal
rate of substitution) in the
theory of demand. The similar concept is used in the
explanation of producers equilibrium and is named as
marginal rate of technical substitution (MRTS).
Marginal rate of technical
substitution (MRTS) is:
"The rate at which one factor can be
substituted for another while holding the level of output
constant".
The slope of an isoquant shows the
ability of a firm to replace one factor with another while
holding the output constant. For example, if 2 units of factor
capital (K) can be replaced by 1 unit of labor (L), marginal
rate of technical substitution will be thus:
MRS = ΔK = 2 = 2
ΔL
1
Explanation:
The concept of MRTS can be explained
easily with the help of the table and the graph, below:
Schedule:
|
Factor Combinations
|
Units of Labor
|
Units of Capital
|
Units of Output of Commodity
X |
MRTS of Labor for Capital
|
|
A |
1 |
15 |
150 |
- |
|
B |
2 |
11 |
150 |
4:1 |
|
C |
3 |
8 |
150 |
3:1 |
|
D |
4 |
6 |
150 |
2:1 |
|
E |
5 |
5 |
150 |
1:1 |
It is clear from the above table
that all the five different combinations of labor and capital
that is A, B, C, D and E yield the same level of output of 150
units of commodity X, As we move down from factor A to factor B,
then 4 units of capital are required for obtaining 1 unit of
labor without affecting the total level of output (150 units of
commodity X).
The MRTS is 4:1. As we step down from factor
combination B to factor combination C, then 3 units of capital
are needed to get 1 unit of labor. The MRTS of labor for capital
3:1. If we further switch down from factor combination C to D,
the MRTS of labor for capital is 2:1. From factor D to E
combination, the MRTS of labor for capital falls down to 1:1.
Formula:
MRTSLK = ΔK
ΔL
It means that the marginal rate of
technical substitution of factor labor for factor capital (K) (MRTSLK)
is the number of units of factor capital (K) which can be
substituted by one unit of factor labor (L) keeping the same
level of output. In the figure 12.8, all the five combinations
of labor and capital which are A, B, C, D and E are plotted on a
graph.
Diagram/Graph:
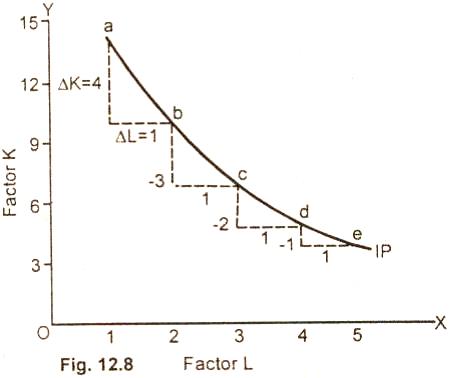
The points A, B, C, D and E are joined to form an isoquant. The iso-product curve shows the whole range of factor
combinations producing 150 units of commodity X. It is important
to point out that ail the five factor combination of labor and
capital on an iso-product curve are technically efficient
combinations. The producer is indifferent towards these,
combinations as these produce the same level of output.
Diminishing
Marginal Rate of Technical Substitution:
The decline in MRTS along an
isoquant for producing the same
level of output is named as diminishing marginal rates of
technical education. As we have seen in Fig. 12.8, that when a
firm moves down from point (a) to point (b) and it hires one
more labor, the firm gives up 4 units of capital (K) and yet
remains on the same isoquant at point (b). So the MRTS is 4. If
the firm hires another labor and moves from point (b) to (c),
the firm can reduce its capital (K) to 3 units and yet remain on
the same isoquant. So the MRTS is 3. If the firm moves from
point (C) to (D), the MRTS is 2 and from point D to e, the MRTS
is 1. The decline in MRTS along an isoquant as the firm
increases labor for capital is called Diminishing Marginal Rate
of Technical Substitution.
Relevant Articles:
|