Properties of Isoquants:
The main properties of the
isoquants are similar to
those of indifference curves. These properties are now discussed
in brief:
(i) An Isoquant Slopes Downward from
Left to Right:
This implies that the Isoquant is a
negatively sloped curve. This is because when the quantify of
factor K (capital) is increased, the quantity of L (labor) must
be reduced so as to keep the same level of output.
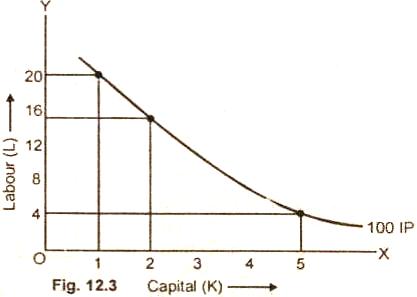
The figure (12.3) depicts that an isoquant IP is negatively sloped curve.
This curve shows that as the amount of factor K is increased
from one unit to 2 units, the units of factor L are decreased
from 20 to 15 only so that output of 100 units remains constant.
(ii) An Isoquant that Lies Above
and to the Right of Another Represents a Higher Output Level:
It means a higher isoquant
represents higher level of output.
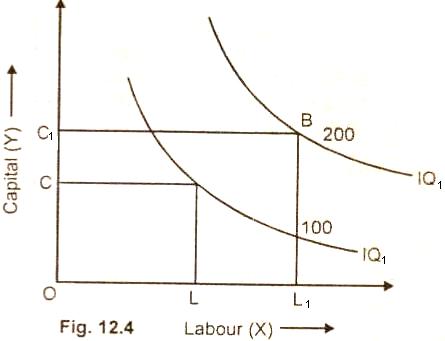
The figure 12.4 represents
this property. It shows that greater output can be secured by increasing the
quantity combinations of both the factors X and Y. The producer
increases the output from 100 units to 200 units by increasing
the quantity combination of both the X and Y. The combination of OC of capital and OL of labor yield 100 units of production. The
production can be increased to 200 units by increasing the
capital from OC to OC1 and labor from OL to OL1.
(iii) Isoquants Cannot Cut Each
Other:
The two isoquants can not intersect
each other.

If two isoquant are drawn to intersect each other as
is shown in this figure 12.5, then it is a negation of the
property that higher Isoquant represents higher level of output
to a lower Isoquant. The intersection at point E shows that the
same factor combination can produce 100 units as well as 200
units. But this is quite absurd. How can the same level of
factor combination produce two different levels of output, when
the technique of production remains unchanged. Hence two
isoquants cannot intersect each other.
(iv) Isoquants are Convex to the
Origin:
This property implies that the
marginal significance of one factor in terms of another factor
diminishes along an ISO product curve. In other words, the
isoquants are convex to the origin due to diminishing marginal
rate of substitution.
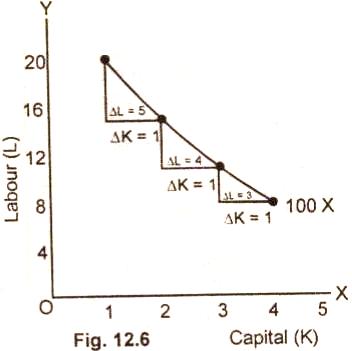
In this figure 12.6 MRSKL
diminishes from 5:1 to 4:1 and further to 3:1. This shows that
as more and more units of capital (K) are employed to produce
100 units of the product, lesser and lesser units of labor (L)
are used. Hence diminishing marginal rate of technical
substitution is the reason for the convexity of an isoquant.
(v) Each Isoquant is Oval Shaped:
The iso product curve, is
elliptical. This means that the firm produces only those
segments of the iso-product curves which are convex to the
origin and lie between the ridge lines. This is the economic
region of production.
Relevant Articles:
|