Law of Returns to Scale:
Definition and Explanation:
The law of returns are often
confused with the law of returns to scale. The law of
returns operates in the short period. It explains the production
behavior of the firm with one factor variable while other
factors are kept constant. Whereas the law of returns to
scale operates in the long period. It explains the production
behavior of the firm with all variable factors.
There is no fixed factor of
production in the long run. The law of returns to scale
describes the relationship between variable inputs and output
when all the inputs, or factors are increased in the same
proportion. The law of returns to scale analysis the effects of
scale on the level of output. Here we find out in what
proportions the output changes when there is proportionate
change in the quantities of all inputs. The answer to this
question helps a firm to determine its scale or size in the long
run.
It has been observed that when there
is a proportionate change in the amounts of inputs, the behavior
of output varies. The output may increase by a great proportion,
by in the same proportion or in a smaller proportion to its
inputs. This behavior of output with the increase in scale of
operation is termed as increasing returns to scale, constant
returns to scale and diminishing returns to scale. These three
laws of returns to scale are now explained, in brief, under
separate heads.
(1) Increasing Returns to Scale:
If the output of a firm increases
more than in proportion to an equal percentage increase in all
inputs, the production is said to exhibit increasing returns to
scale.
For example, if the amount of
inputs are doubled and the output increases by more than double,
it is said to be an increasing returns returns to scale. When
there is an increase in the scale of production, it leads to
lower average cost per unit produced as the firm enjoys
economies of scale.
(2) Constant Returns to Scale:
When all inputs are increased by a
certain percentage, the output increases by the same percentage,
the production function is said to exhibit constant returns to
scale.
For example, if a firm
doubles inputs, it doubles output. In case, it triples output.
The constant scale of production has no effect on average cost
per unit produced.
(3) Diminishing Returns to Scale:
The term 'diminishing' returns to
scale refers to scale where output increases in a smaller
proportion than the increase in all inputs.
For example, if a firm
increases inputs by 100% but the output decreases by less than
100%, the firm is said to exhibit decreasing returns to scale.
In case of decreasing returns to scale, the firm faces
diseconomies of scale. The firm's scale of production leads to
higher average cost per unit produced.
Graph/Diagram:
The three laws of returns to scale
are now explained with the help of a graph below:
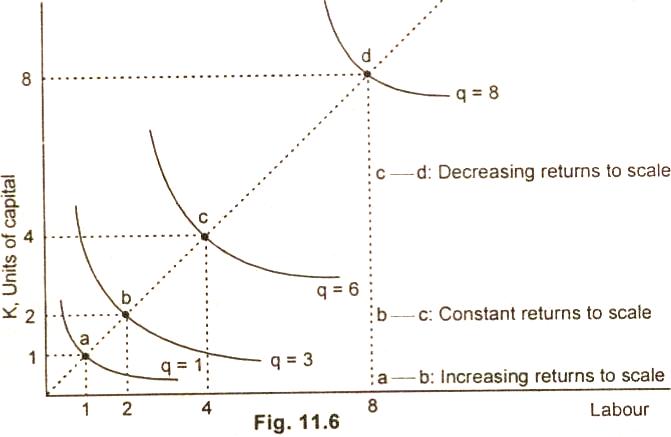
The figure 11.6 shows that when a
firm uses one unit of labor and one unit of capital, point a, it
produces 1 unit of quantity as is shown on the q = 1 isoquant.
When the firm doubles its outputs by using 2 units of labor and
2 units of capital, it produces more than double from
q = 1 to q = 3.
So the production function has
increasing returns to scale in this range. Another output from
quantity 3 to quantity 6. At the last doubling point c to point
d, the production function has decreasing returns to scale. The
doubling of output from 4 units of input, causes output to
increase from 6 to 8 units increases of two units only.
Relevant Articles:
|